2019年09月12日
阅读: 3950
八大排序算法的Python实现
友情提醒:本文最后更新于 2355 天前,文中所描述的信息可能已发生改变,请谨慎使用。
一、冒泡排序
冒泡排序重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。 这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端,故名。
步骤:
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
代码实现:
# -*- coding:utf-8 -*-
def bubble_sort(nums):
for i in range(len(nums) - 1): # 遍历 len(nums)-1 次
for j in range(len(nums) - i - 1): # 已排好序的部分不用再次遍历
if nums[j] > nums[j+1]:
nums[j], nums[j+1] = nums[j+1], nums[j] # Python 交换两个数不用中间变量
return nums
# 测试
data_test = [10, 23, 1, 53, 654, 54, 16, 646, 65, 3155, 546, 31]
sorted_list = bubble_sort(data_test)
print(sorted_list)
二、选择排序
从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
代码实现:
# -*- coding:utf-8 -*-
def select_sort(raw_list):
length = len(raw_list)
for index in range(length):
for i in range(index, length):
if raw_list[index] > raw_list[i]:
raw_list[index], raw_list[i] = raw_list[i], raw_list[index]
return raw_list
# 测试
data_test = [10, 23, 1, 53, 654, 54, 16, 646, 65, 3155, 546, 31]
sorted_list = select_sort(data_test)
print(sorted_list)
三、插入排序
每步将一个待排序的纪录,按其关键码值的大小插入前面已经排序的文件中适当位置上,直到全部插入完为止。
步骤:
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5
代码实现:
# -*- coding:utf-8 -*-
def insert_sort(raw_list):
length = len(raw_list)
for i in range(1, length):
temp = raw_list[i]
#j从i-1 到 0倒序
for j in range(i-1,-1,-1):
if(raw_list[j]<=temp):
break
if(raw_list[j]>temp):
raw_list[j], raw_list[j+1] = temp, raw_list[j]
return raw_list
# 测试
data_test = [10, 23, 1, 53, 654, 54, 16, 646, 65, 3155, 546, 31]
sorted_list = insert_sort(data_test)
print(sorted_list)
四、希尔排序
先取一个小于n的整数d1作为第一个增量,把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量d2<d1重复上述的分组和排序,直至所取的增量
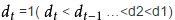
即所有记录放在同一组中进行直接插入排序为止。
代码实现:
# -*- coding:utf-8 -*-
def shell_sort(list):
length = len(list)
dist = length/2
while dist > 0:
for i in range(dist, length):
temp = list[i]
j = i
while j >= dist and temp < list[j-dist]:
list[j] = list[j-dist]
j -= dist
list[j] = temp
dist /= 2
return list
# 测试
list = [10, 23, 1, 53, 654, 54, 16, 646, 65, 3155, 546, 31]
print shell_sort(list)
五、归并排序
归并排序,就是把两个已经排列好的序列合并为一个序列。
代码实现:
# -*- coding:utf-8 -*-
# 算法逻辑比较简单,以第一个list为基准,第二个向第一个插空
def merge_sort(list1, list2):
length_list1 = len(list1)
length_list2 = len(list2)
list3 = []
j = 0
for i in range(length_list1):
while list2[j] < list1[i] and j < length_list2:
list3.append(list2[j])
j = j + 1
list3.append(list1[i])
if j < (length_list2 - 1):
for k in range(j, length_list2):
list3.append(list2[k])
return list3
# 测试
list1 = [1,3,5,10]
list2 = [2,4,6,8,9,11,12,13,14]
print merge_sort(list1, list2)
六、快速排序
代码实现:
# 递归实现
def quick_sort(nums):
if len(nums) <= 1:
return nums
pivot = nums[0] # 基准值
left = [nums[i] for i in range(1, len(nums)) if nums[i] < pivot]
right = [nums[i] for i in range(1, len(nums)) if nums[i] >= pivot]
return quickSort(left) + [pivot] + quickSort(right)
# 随意选择一个数字作为基准,比基准数字大的在右,比基准数字小的在左。
# -*- coding:utf-8 -*-
def kp(arr, i, j): # 快排总函数
# 制定从哪开始快排
if i < j:
base = kpgc(arr, i, j)
kp(arr, i, base)
kp(arr, base + 1, j)
def kpgc(arr, i, j): # 快排排序过程
base = arr[i]
while i < j:
while i < j and arr[j] >= base:
j -= 1
while i<j and arr[j] < base:
arr[i] = arr[j]
i += 1
arr[j] = arr[i]
arr[i] = base
return i
ww = [3,2,4,1,59,23,13,1,3]
print ww
kp(ww, 0, len(ww) - 1)
print ww
七、堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
步骤:
- 创建最大堆:将堆所有数据重新排序,使其成为最大堆
- 最大堆调整:作用是保持最大堆的性质,是创建最大堆的核心子程序
- 堆排序:移除位在第一个数据的根节点,并做最大堆调整的递归运算
代码实现:
# -*- coding:utf-8 -*-
def head_sort(list):
length_list = len(list)
first = int(length_list / 2 - 1)
for start in range(first, -1, -1):
max_heapify(list, start, length_list - 1)
for end in range(length_list - 1, 0, -1):
list[end], list[0] = list[0], list[end]
max_heapify(list, 0, end-1)
return list
def max_heapify(ary, start, end):
root = start
while True:
child = root*2 + 1
if child > end:
break
if child + 1 <= end and ary[child]<ary[child + 1]:
child = child + 1
if ary[root] < ary[child]:
ary[root], ary[child] = ary[child], ary[root]
root = child
else:
break
# 测试:
list = [10, 23, 1, 53, 654, 54, 16, 646, 65, 3155, 546, 31]
print head_sort(list)
八、基数排序
# -*- coding:utf-8 -*-
def count_sort(list):
max = min = 0
for i in list:
if i < min:
min = i
if i > max:
max = i
count = [0] * (max - min +1)
for j in range(max - min + 1):
count[j] = 0
for index in list:
count[index-min] += 1
index = 0
for a in range(max - min + 1):
for c in range(count[a]):
list[index] = a + min
index += 1
return list
# 测试:
list = [10, 23, 1, 53, 654, 54, 16, 646, 65, 3155, 546, 31]
print count_sort(list)
附:各种算法对应的时间复杂度和空间复杂度


